等边/任意三角形的内三角形最小周长
等边三角形的内三角形最小周长
今天弟弟问了一道初中数学题:
三角形 ABC 是一个等边三角形,动点 P、M、N 分别在线段 AB、BC、AC 上运动,三角形 ABC 边长是 2,求三角形 PMN 的周长最小值。
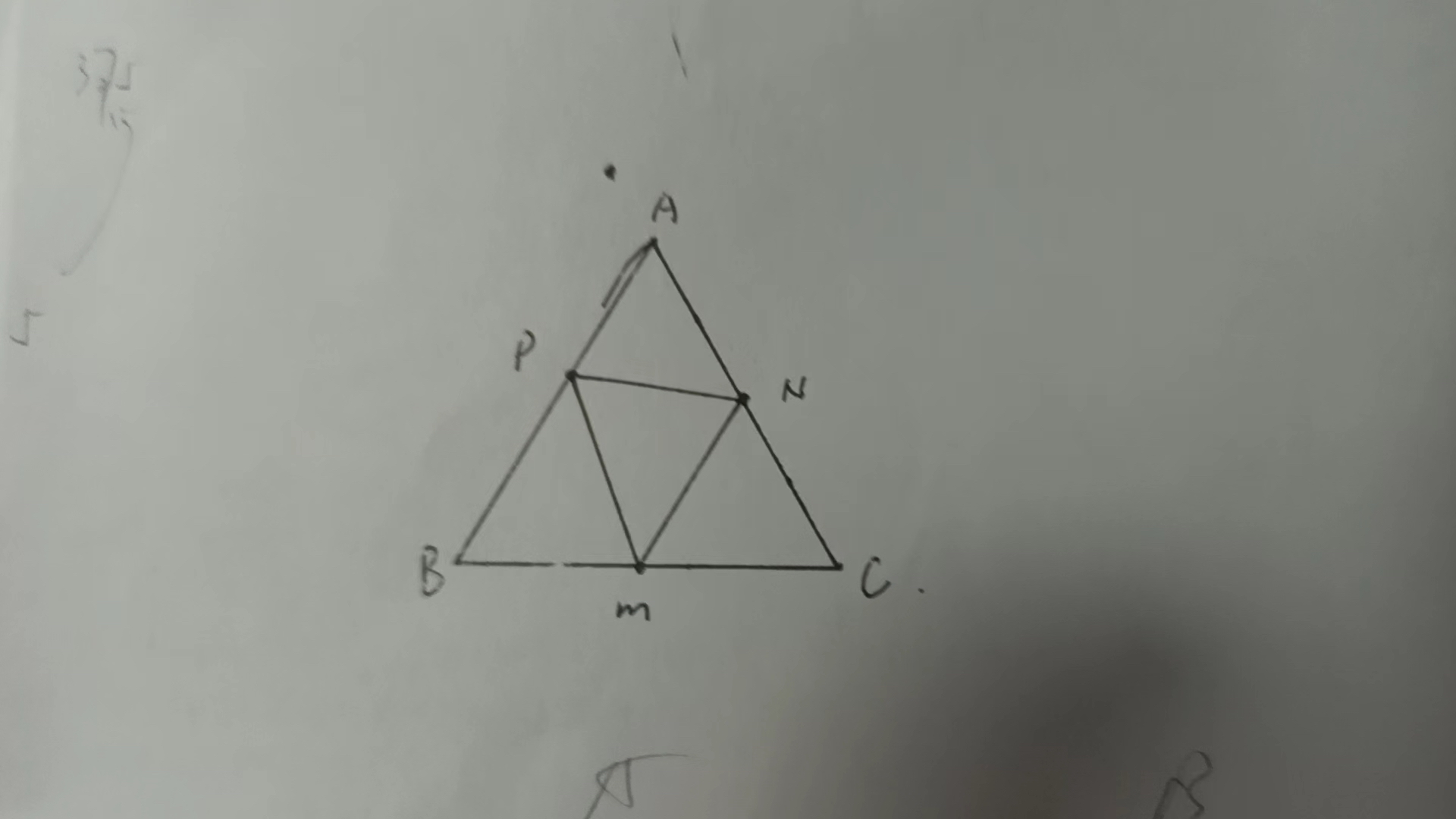
题目可以概括为 等边三角形的内三角形最小周长,其解题思路和将军饮马问题一脉相承。
在解答这道题之前,可先尝试解答其更通用的形式:任意三角形的内三角形最小周长。
任意三角形的内三角形最小周长
思路源于知乎专栏 https://zhuanlan.zhihu.com/p/112601281。
结论:
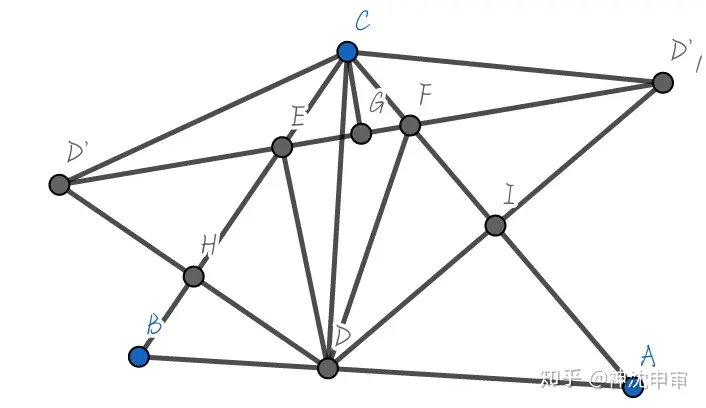
满足最小周长条件的三角形三个点都是原三角形三个顶点过其对边引的垂线的垂足。
$$
\begin{align*}
& 作 CD \bot AB;\newline
& D^{‘} 和 D^{‘}_1 分别是点 D 关于 BC 和 AC 的轴对称点; \newline
& CG 是 D^{‘} D^{‘}_1 的垂线 \newline
\newline
证明:& \because D^{‘} 是点 D 关于 BC 的轴对称点 \newline
& \therefore CD = CD^{‘} \newline
同理 & \because D^{‘}_1 是点 D 关于 AC 的轴对称点 \newline
& \therefore CD = CD^{‘}_1 \newline
& \therefore CD^{‘} = CD^{‘}_1 \newline
& \therefore \angle CD^{‘}G = CD^{‘}_1G \newline
又 & \because CG 是 D^{‘} D^{‘}_1 的垂线 \newline
& \therefore D^{‘}G = CD^{‘}cos \angle CD^{‘}G, D^{‘}_1G = CD^{‘}_1cos \angle CD^{‘}_1G \newline
& \therefore D^{‘}D^{‘}_1 = 2D^{‘}G = 2CD^{‘}cos \angle CD^{‘}G = 2CDcos \angle CD^{‘}G \newline
\newline
& 已知 \because \angle ECF 一定 \newline
& \therefore \angle CEF + \angle CFE 一定 \newline
& \therefore \angle D^{‘}CE + \angle CD^{‘}G + \angle D^{‘}_1CF + \angle CD^{‘}_1G 一定 \newline
又 & \angle ECF 一定 \newline
& \therefore \angle DCE + \angle DCF 一定 \newline
& \because D^{‘} 和 D^{‘}_1 分别是点 D 关于 BC 和 AC 的轴对称点 \newline
& \therefore \angle DCE = \angle D^{‘}CE, \angle DCF = \angle D^{‘}_1CF \newline
& \therefore \angle D^{‘}CE + \angle D^{‘}_1CF 一定 \newline
& \therefore \angle CD^{‘}G + \angle CD^{‘}_1G 一定,且已证 \angle CD^{‘}G = CD^{‘}_1G \newline
& \therefore \angle CD^{‘}G 一定 \newline
\newline
又 & \because D^{‘} 和 D^{‘}_1 分别是点 D 关于 BC 和 AC 的轴对称点 \newline
& \therefore ED = ED^{‘}, FD = FD^{‘}_1 \newline
& \therefore C_\triangle DEF = ED + EF + FD = ED^{‘} + EF + FD^{‘}_1 = D^{‘}D^{‘}_1 = 2CDcos \angle CD^{‘}G \newline
\newline
& \because CD \bot AB \newline
& \therefore 此时点 D 满足 CD 为最短线段,且已证 \angle CD^{‘}G 一定 \newline
& \therefore 此时 C_\triangle DEF 最小 \newline
\end{align*}
$$
总结
在完成上述证明后,取一特殊情况,即该三角形为等边三角形,那么满足最小周长条件的目标三角形的三个点正好位于其所在线段的中点。